Research
I am interested in various problems in discrete mathematics and probability including their applications in social and economic sciences and computer science. Below I describe a couple of directions I have been pursuing recently.
Coding theory
Error-correcting codes are used to make data resistant to errors. Reed-Muller codes are a family of error-correcting codes based on a natural algebraic idea. They are one of the first families of binary codes studied in the information theory, discovered in the 1950s. Despite continuing interest, it is conjectured, but still not proved, that they “achieve capacity” (meaning that they correct errors at the best rate possible given Shannon’s theorem) on the binary symmetric channel, which is one of the most natural noise models. I have been interested in making progress on this problem (see, eg., this preprint).
Social choice theory
Social choice theory studies models of opinion formation and evolution in groups, and how these opinions can be aggregated into decisions.
I was involved in a work that proposed a new model of opinion polarization, a mechanism where the opinions tend to become extreme opposites. Our model uses a geometric setting to capture how polarization happens as a result of interactions between opinions on different subjects.
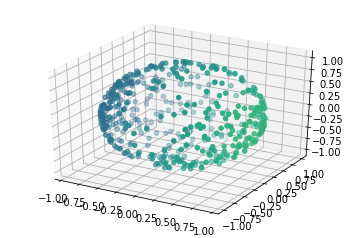
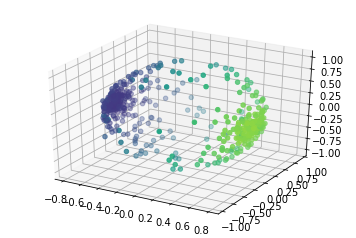
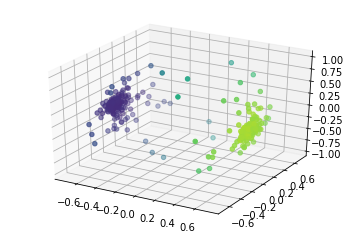
 In another pair of
papers,
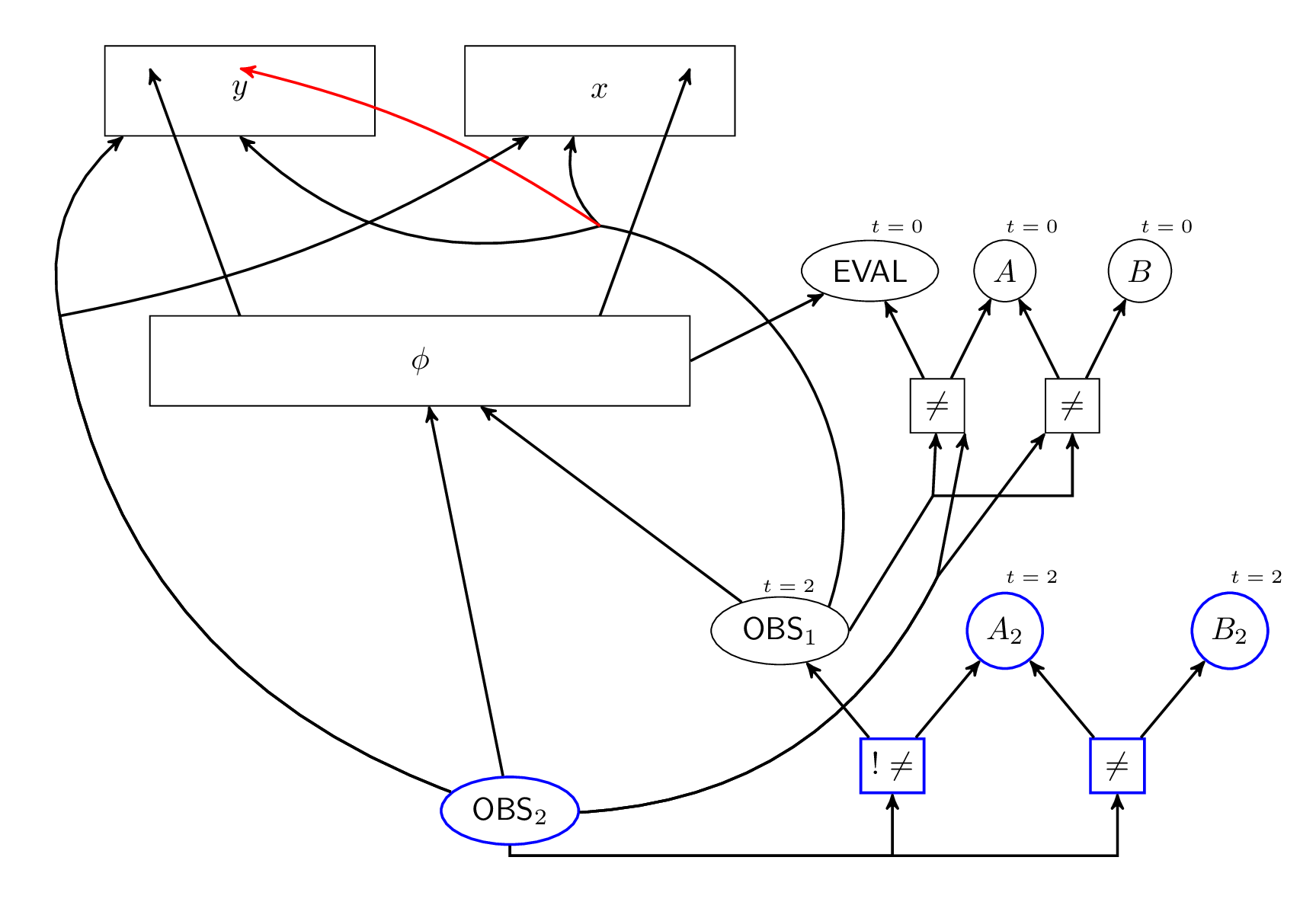
we studied opinion exchange on networks by rational (Bayesian) agents.
This refers to a process where the agents keep updating their opinions
on a subject while reacting to updated opinions of their neighbors. Similarly
as in Aumann agreement theorem, which is a fundamental result in economics,
it is known that the agents eventually converge to consensus. However, we
showed that the computations that the agents require to implement the
rational opinion exchange are so hard as to be infeasible in practice.
Our work supports the belief that assuming perfect rationality in such models
is unrealistic.
In another pair of
papers,
we studied opinion exchange on networks by rational (Bayesian) agents.
This refers to a process where the agents keep updating their opinions
on a subject while reacting to updated opinions of their neighbors. Similarly
as in Aumann agreement theorem, which is a fundamental result in economics,
it is known that the agents eventually converge to consensus. However, we
showed that the computations that the agents require to implement the
rational opinion exchange are so hard as to be infeasible in practice.
Our work supports the belief that assuming perfect rationality in such models
is unrealistic.
Combinatorics
 I am interested in various topics in combinatorics. One example is a study
of intransitive dice. These are dice which do not satisfy transitivity,
in the sense that, for example, in one throw A is more likely to roll a
higher face than B, B is more likely to roll higher than C, but C is more
likely to roll higher than A. In
two
works
we studied quantitative aspects of intransitive dice,
asking how commonly such examples occur in natural
random settings.
I am interested in various topics in combinatorics. One example is a study
of intransitive dice. These are dice which do not satisfy transitivity,
in the sense that, for example, in one throw A is more likely to roll a
higher face than B, B is more likely to roll higher than C, but C is more
likely to roll higher than A. In
two
works
we studied quantitative aspects of intransitive dice,
asking how commonly such examples occur in natural
random settings.
